Mathematica と 2013-12-20-wheezy-raspbian (2013/12/26)
Raspberry Pi 専用の Linux ディストリビューション である Raspbian の新イメージ 2013-12-20-wheezy-raspbian が 2013/12/24 に 公開されました。 例によって Raspbian の新イメージ(2013-12-20-wheezy-raspbian) をインストールしてみます。
今回は Linux カーネルのバージョンが 3.6.11+ から 3.10.24+ に上がっています。 また数式処理ソフトの Wolfram Mathematica が含まれるようになりました。昔、仕事でMacintoshII 上で Mathematica を使ったことがありますが、マシンと合わせて200万円近かった気がします。4000円ほどのRaspberry Pi上で無料で Mathematica 使えるようになってしまいました。Linux上ではオープンソースの数式処理ソフトのMaximaが使えるので、すでに数式処理ソフトにお金をかけなくてもよくなっていますが。
2013-12-20-wheezy-raspbian のインストール
すでにRaspberry Pi で Raspbian を使っていれば、次のコマンドでも新イメージと同じ環境がインストールできるはずです。 しかし、ここでは別のSDカードに 2013-09-25-wheezy-raspbian をインストールすることにします。以下の作業を行った SD カードはデータがすべて初期化されるので、新しいカードやデータが不要なSDカードを使って下さい。
sudo apt-get update sudo apt-get upgrade
MacBook Pro17 の MacOSX 10.8.5 でインストール作業した記録です。 MacOS X ではデバイス名の指定方法が異なるだけで、Linuxと同じく dd コマンドを使ってSDカードに ディスクイメージを書き込みます。まずは SDカードのデバイス名を調べます。以下の例は、私のMacBookでの例です。適宜読み替えてください。
dd コマンドのデバイスの指定を間違えると最悪ハードディスクがすべて消えるなどの悲惨な結果が待っています。十分に注意して行なってください。
$ uname -rsv
Darwin 13.0.0 Darwin Kernel Version 13.0.0: Thu Sep 19 22:22:27 PDT 2013;
root:xnu-2422.1.72~6/RELEASE_X86_64
「sudo apt-get update && apt-get upgrade」でもほとんどの機能がインストールされるようですが、安全に別のSDカードに 2013-12-20-wheezy-raspbian をインストールしました。 ダウンロードしたディスクイメージは以下のサイズです。
$ ls -lt 2013-12-20-wheezy-raspbian.zip
-rw-r--r--@ 1 jun staff 821753441 12 24 20:51 2013-12-20-wheezy-raspbian.zip
イメージのハッシュ(SHA-1 Checksum)が公式サイトにある ade48c874f8e4b694175de4c87d7357960961fbf であることを確認しました。
$ shasum 2013-12-20-wheezy-raspbian.zip
ade48c874f8e4b694175de4c87d7357960961fbf 2013-12-20-wheezy-raspbian.zip
いつものようにMacBook Pro17 にUSB接続のmicroSDカードリーダ
$ df 略 /dev/disk1s2 30687672 3885144 25503368 14% 75625 882087 8% /Volumes/Untitled /dev/disk1s1 114576 37184 77392 33% 512 0 100% /Volumes/boot $ diskutil unmount /dev/disk1s1 Volume boot on disk1s1 unmounted $ diskutil unmount /dev/disk1s2 Volume on disk1s2 unmounted
古いイメージが入っていた 16GBのclass 10 microSDカード
$ sudo fdisk -i /dev/disk1
Password:
fdisk: could not open MBR file /usr/standalone/i386/boot0: No such file or directory
-----------------------------------------------------
------ ATTENTION - UPDATING MASTER BOOT RECORD ------
-----------------------------------------------------
Do you wish to write new MBR and partition table? [n] y
パーティションを確認。
$ sudo fdisk /dev/disk1
Disk: /dev/disk1 geometry: 1947/255/63 [31291392 sectors]
Signature: 0xAA55
Starting Ending
#: id cyl hd sec - cyl hd sec [ start - size]
------------------------------------------------------------------------
*1: AB 0 1 1 - 1023 254 63 [ 63 - 16384] Darwin Boot
2: AF 1023 254 63 - 1023 254 63 [ 16447 - 31274945] HFS+
3: 00 0 0 0 - 0 0 0 [ 0 - 0] unused
4: 00 0 0 0 - 0 0 0 [ 0 - 0] unused
zipファイルを展開します。
$ unzip 2013-12-20-wheezy-raspbian.zip Archive: 2013-12-20-wheezy-raspbian.zip inflating: 2013-12-20-wheezy-raspbian.img $ ls -lt 2013-12-20-wheezy-raspbian* -rw-r--r--@ 1 jun staff 821753441 12 24 20:51 2013-12-20-wheezy-raspbian.zip -rw-r--r--@ 1 jun staff 2962227200 12 21 06:16 2013-12-20-wheezy-raspbian.img
SDカードに書き込みます。
$ sudo time dd bs=1m if=2013-12-20-wheezy-raspbian.img of=/dev/rdisk1
2825+0 records in
2825+0 records out
2962227200 bytes transferred in 152.449187 secs (19430915 bytes/sec)
152.60 real 0.00 user 1.89 sys
ブート領域のファイルを確認します。
$ cd /Volumes/boot $ ls -lt total 38128 -rwxrwxrwx 1 jun staff 137 12 20 21:09 issue.txt -rwxrwxrwx 1 jun staff 142 12 20 20:08 cmdline.txt -rwxrwxrwx 1 jun staff 1180 12 20 20:08 config.txt -rwxrwxrwx 1 jun staff 17824 12 20 11:05 bootcode.bin -rwxrwxrwx 1 jun staff 5778 12 20 11:05 fixup.dat -rwxrwxrwx 1 jun staff 2062 12 20 11:05 fixup_cd.dat -rwxrwxrwx 1 jun staff 8811 12 20 11:05 fixup_x.dat -rwxrwxrwx 1 jun staff 3113896 12 20 11:05 kernel.img -rwxrwxrwx 1 jun staff 9791576 12 20 11:05 kernel_emergency.img -rwxrwxrwx 1 jun staff 2513844 12 20 11:05 start.elf -rwxrwxrwx 1 jun staff 480056 12 20 11:05 start_cd.elf -rwxrwxrwx 1 jun staff 3492228 12 20 11:05 start_x.elf -rwxrwxrwx 1 jun staff 18974 9 25 21:57 LICENSE.oracle
/boot/config.txt を確認してみます。バージョンアップでも特に変更されていません。
$ cat -n config.txt
1 # uncomment if you get no picture on HDMI for a default "safe" mode
2 #hdmi_safe=1
3
4 # uncomment this if your display has a black border of unused pixels visible
5 # and your display can output without overscan
6 #disable_overscan=1
7
8 # uncomment the following to adjust overscan. Use positive numbers if console
9 # goes off screen, and negative if there is too much border
10 #overscan_left=16
11 #overscan_right=16
12 #overscan_top=16
13 #overscan_bottom=16
14
15 # uncomment to force a console size. By default it will be display's size minus
16 # overscan.
17 #framebuffer_width=1280
18 #framebuffer_height=720
19
20 # uncomment if hdmi display is not detected and composite is being output
21 #hdmi_force_hotplug=1
22
23 # uncomment to force a specific HDMI mode (this will force VGA)
24 #hdmi_group=1
25 #hdmi_mode=1
26
27 # uncomment to force a HDMI mode rather than DVI. This can make audio work in
28 # DMT (computer monitor) modes
29 #hdmi_drive=2
30
31 # uncomment to increase signal to HDMI, if you have interference, blanking, or
32 # no display
33 #config_hdmi_boost=4
34
35 # uncomment for composite PAL
36 #sdtv_mode=2
37
38 #uncomment to overclock the arm. 700 MHz is the default.
39 #arm_freq=800
40
41 # for more options see https://elinux.org/RPi_config.txt
SDカードをアンマウントして取り出します。
$ df 略 /dev/disk1s1 114576 38192 76384 34% 512 0 100% /Volumes/boot /dev/disk1s2 5573760 4267168 1023456 81% 78594 98462 44% /Volumes/Untitled $ diskutil unmount /dev/disk1s1 Volume boot on disk1s1 unmounted $ diskutil unmount /dev/disk1s2 Volume on disk1s2 unmounted
新しいイメージで起動
インストールしたSDカードをRaspberry Piにセットして起動。 最初の起動時に設定画面が表示されますが、前のバージョンから変わっていないので、前回の 2013-09-25-wheezy-raspbian の設定画面の解説を参考にして下さい。
Mathematica
今回のRaspbianイメージに最初から含まれるようになった Wolfram Mathematica は数式処理を行うアプリケーションです。 コンピュータは数値計算はべらぼうに速いですが、因数分解や展開といった式の変形はしてくれません。 Mathematica や Maxima はこの数式処理に使うソフトウェアです。
使い方はMathematica数値数式プログラミング
Mathematica の起動
Mathematica はRaspberry Piのデスクトップの左上にアイコンが表示されていて、クリックすると起動します。 グラフも表示できるウィンドウが開いて GUI で操作できますが、ここではリモートからも SSH 越しに操作できるようにコンソールで使う方法を紹介します。
$ /opt/Wolfram/WolframEngine/10.0/Executables/math
Wolfram Language (Raspberry Pi Pilot Release)
Copyright 1988-2013 Wolfram Research
Information & help: wolfram.com/raspi
In[1]:=
/opt/Wolfram/WolframEngine/10.0/Executables ディレクトリにある math コマンドを実行すると、コンソールから式を入力できるようになります。「In[1]:=」のあとに式を入力すると、対応する番号の 「Out[1]=」に結果が表示されます。
数式の展開と因数分解
展開は Expand[式] と 因数分解は Factor[式] で簡単に求めることができます。 宿題では使わないように。
In[1]:= Expand[ (x + a)(x + b) ] 2 Out[1]= a b + a x + b x + x In[2]:= Factor[Out[1]] Out[2]= (a + x) (b + x) In[3]:= Expand[ (a - b)^3 ] 3 2 2 3 Out[3]= a - 3 a b + 3 a b - b In[4]:= Factor[ a^3 - 3 a^2 b + 3 a b^2 - b^3 ] 3 Out[4]= (a - b)
行列の演算
前に3次元コンピュータグラフィックスで必要となる行列計算について解説しましたが、その中で行列の乗算について下の式を紹介しました。
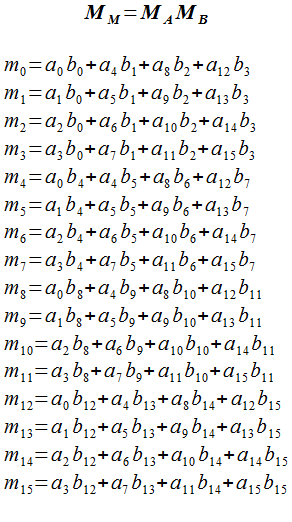
実はこの式は Maxima で計算したものを加工しています。こういった面倒な計算は数式処理ソフトにやってもらうのが楽です。下の実行例では a0 といった下付きの添え字を付加するのに Subscript を使っているのでちょっと複雑に見えますが、行列を上の行から順次中括弧に入れて並べているだけです。
In[1]:= mata = {{Subscript[a,0],Subscript[a,4],Subscript[a,8],Subscript[a,12]}, {Subscript[a,1],Subscript[a,5],Subscript[a,9],Subscript[a,13]}, {Subscript[a,2],Subscript[a,6],Subscript[a,10],Subscript[a,14]}, {Subscript[a,3],Subscript[a,7],Subscript[a,11],Subscript[a,15]}} Out[1]= {{a , a , a , a }, {a , a , a , a }, {a , a , a , a }, 0 4 8 12 1 5 9 13 2 6 10 14 > {a , a , a , a }} 3 7 11 15 In[2]:= matb = {{Subscript[b,0],Subscript[b,4],Subscript[b,8],Subscript[b,12]}, {Subscript[b,1],Subscript[b,5],Subscript[b,9],Subscript[b,13]}, {Subscript[b,2],Subscript[b,6],Subscript[b,10],Subscript[b,14]}, {Subscript[b,3],Subscript[b,7],Subscript[b,11],Subscript[b,15]}} Out[2]= {{b , b , b , b }, {b , b , b , b }, {b , b , b , b }, 0 4 8 12 1 5 9 13 2 6 10 14 > {b , b , b , b }} 3 7 11 15
これで mata と matb という変数にそれぞれ要素が a0 から a15 と b0 から b15 の 4行4列の行列を設定しています。 この行列の乗算はこれで mata と matb の間にピリオドを置けば計算されます。
In[3]:= mata . matb
Out[3]= {{a b + a b + a b + a b , a b + a b + a b + a b ,
0 0 4 1 8 2 12 3 0 4 4 5 8 6 12 7
> a b + a b + a b + a b , a b + a b + a b + a b },
0 8 4 9 8 10 12 11 0 12 4 13 8 14 12 15
> {a b + a b + a b + a b , a b + a b + a b + a b ,
1 0 5 1 9 2 13 3 1 4 5 5 9 6 13 7
> a b + a b + a b + a b , a b + a b + a b + a b },
1 8 5 9 9 10 13 11 1 12 5 13 9 14 13 15
> {a b + a b + a b + a b , a b + a b + a b + a b ,
2 0 6 1 10 2 14 3 2 4 6 5 10 6 14 7
> a b + a b + a b + a b , a b + a b + a b + a b },
2 8 6 9 10 10 14 11 2 12 6 13 10 14 14 15
> {a b + a b + a b + a b , a b + a b + a b + a b ,
3 0 7 1 11 2 15 3 3 4 7 5 11 6 15 7
> a b + a b + a b + a b , a b + a b + a b + a b }}
3 8 7 9 11 10 15 11 3 12 7 13 11 14 15 15
In[4]:=
CPUがいまいち非力なRaspberry Piでも一瞬で計算できます。上の図中のm0 から m15 と一致していることが確認できます。
回転行列
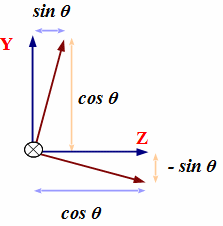
X軸回りに角度 x で回転させる 4x4行列に rotx という名前をつけます。
 |
 |
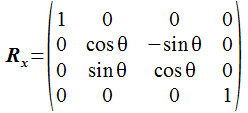In[1]:= rotx = {{1,0,0,0},{0,cos[x],-sin[x],0},{0,sin[x],cos[x],0},{0,0,0,1}}
Out[1]= {{1, 0, 0, 0}, {0, cos[x], -sin[x], 0}, {0, sin[x], cos[x], 0},
> {0, 0, 0, 1}}
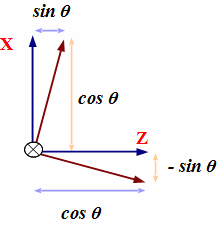
また、角度 y でY軸回りに回転させる行列に roty という名前をつけます。
 |
 |
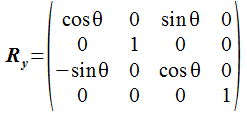In[2]:= roty = {{cos[y],0,sin[y],0},{0,1,0,0},{-sin[y],0,cos[y],0},{0,0,0,1}}
Out[2]= {{cos[y], 0, sin[y], 0}, {0, 1, 0, 0}, {-sin[y], 0, cos[y], 0},
> {0, 0, 0, 1}}
同様に、角度 z でZ軸回りに回転させる行列は次のようになります。
 |
 |
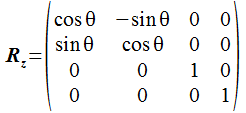In[3]:= rotz = {{cos[z], -sin[z],0,0},{sin[z],cos[z],0,0},{0,0,1,0},{0,0,0,1}}
Out[3]= {{cos[z], -sin[z], 0, 0}, {sin[z], cos[z], 0, 0}, {0, 0, 1, 0},
> {0, 0, 0, 1}}
例えば、頂点をY軸周りに回転させた後、X軸周りに回転させる行列は roty の左側から rotx を乗じた行列になります。OpenGLでは頂点座標は列ベクトルであらわすため、先に頂点を回転させる行列は、ベクトルに近い右側に置くことに注意して下さい。
In[4]:= rotx . roty
Out[4]= {{cos[y], 0, sin[y], 0}, {sin[x] sin[y], cos[x], -(cos[y] sin[x]), 0},
> {-(cos[x] sin[y]), sin[x], cos[x] cos[y], 0}, {0, 0, 0, 1}}
4x4行列同士の乗算は 上で示したように複雑な計算が必要ですが、回転行列に限ると要素に0が多いため、このようにシンプルな結果となる事がわかります。さらにZ軸周りの回転も加えて、Z, Y, X の順に回転させる場合とZ, Y, X の順に回転させる場合も計算してみます。
In[5]:= rotx . roty . rotz Out[5]= {{cos[y] cos[z], -(cos[y] sin[z]), sin[y], 0}, > {cos[z] sin[x] sin[y] + cos[x] sin[z], > cos[x] cos[z] - sin[x] sin[y] sin[z], -(cos[y] sin[x]), 0}, > {-(cos[x] cos[z] sin[y]) + sin[x] sin[z], > cos[z] sin[x] + cos[x] sin[y] sin[z], cos[x] cos[y], 0}, {0, 0, 0, 1}} In[6]:= rotz . roty . rotx Out[6]= {{cos[y] cos[z], cos[z] sin[x] sin[y] - cos[x] sin[z], > cos[x] cos[z] sin[y] + sin[x] sin[z], 0}, > {cos[y] sin[z], cos[x] cos[z] + sin[x] sin[y] sin[z], > -(cos[z] sin[x]) + cos[x] sin[y] sin[z], 0}, > {-sin[y], cos[y] sin[x], cos[x] cos[y], 0}, {0, 0, 0, 1}}
行列は掛け算する順序で結果が異なることが実際に確認できます。こういった計算を実際に紙と鉛筆で計算するのは面倒な上、結果が正しいかどうかに自信が持てないものです。微積分や統計などだけではなく上記のような簡単だけれども面倒な計算にも十分役に立ちます。 高校生諸君、くれぐれも宿題には使わないように!
